Source: BBC
The Beauty of Maths: Fibonacci and the Golden Ratio
Have you ever heard of the Fibonacci sequence? Or the Golden Ratio? Or the Golden Spiral?
These mysterious numbers and shapes are all connected to each other. If you look closely, they can be found in the most unexpected of places, creating beautiful and pleasing patterns.
Put simply, the Fibonacci sequence is a series of numbers which begins with 1 and 1. From there, you add the previous two numbers in the sequence together, to get the next number. This is a type of Recursive Sequence.
So 1+1=2, 1+2=3, 2+3=5, and so on. This gives you a sequence that looks like 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 etc. But what makes this sequence so special and interesting?
The mathematical sequence that governs nature
For starters, Fibonacci numbers can be found in the natural world all around us. Most flowers, for example, will have a number of petals which correspond with the Fibonacci sequence. Irises have three petals whereas wild roses and buttercups have five petals. That is of course, until a petal falls off. No wonder rare four leaf clovers are seen as lucky!
If you cut into a piece of fruit, you’re likely to find a Fibonacci number there as well, in how the sections of seeds are arranged. Bananas have three sections whilst apples have five.
The Fibonacci sequence even plays a role in the subtle spirals you can see in the seed head of a sunflower. This is because of something known as the Golden Ratio, the Golden Section or the Greek letter Phi.
If you take a number in the sequence above 5, and divided it by the previous number, you will get an answer very close to 1.618. The larger the numbers, the closer you get to 1.618. The Golden Ratio is an irrational number, and so cannot be written as a fraction. Again, this is a number that can be found the natural world.
Take the sunflower. To be as efficient as possible, its seeds need to be closely packed together without overlapping. Now, if it simply grew seeds in a straight line in one direction, that would leave loads of empty space on the flower head. The best way of minimising wasted space is for the seeds to grow in spirals, with each seed growing at a slight angle away from the previous one.
If the degree of turn was a fraction, like 1/4, that doesn’t help matters much because after four turns the seed pattern would be right back at the start again. There would be four lines of seeds, but that’s not much better than one when trying to cover a circular area.
The perfect degree of turn needs to be an irrational number, which can’t be easily approximated by a fraction, and the answer is the Golden Ratio.
Transforming numbers into an eye-catching spiral
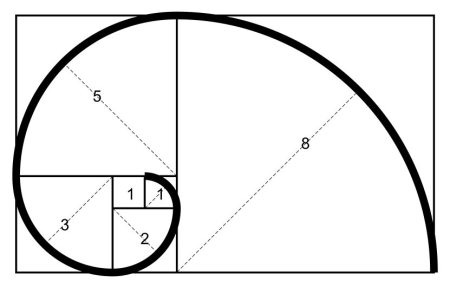
Another way of thinking about the Golden Ratio is as a spiral. This spiral gets wider by a factor of 1.618 every time it makes a quarter turn (90°).
Drawing a perfect Golden Spiral is pretty tricky to do by hand, but just like with the Golden Ratio, you can get a close approximation with the Fibonacci Spiral. This is created by drawing an arc through a series of squares which correspond to the Fibonacci numbers, so 1², 1², 2², 3² etc.
You might have seen these spirals superimposed over famous pieces of artwork, as experts try and explain why we find them so aesthetically pleasing. Often, the spiral draws in our eye so that the focus of the artwork is found in the centre of the spiral. Examples can be found in the works of Leonardo da Vinci and Salvador Dali.
Listening for the Fibonacci sequence in music
Fibonacci (pictured above) didn’t actually discover the sequence himself. Born Leonardo Bonacci in 12th-Century Pisa, Italy, the mathematician travelled extensively around North Africa.
There, he learnt how the Hindu-Arabic numerals of 0-9 could be used to complete calculations more easily than the Roman numerals still in use across much of Europe.
Fibonacci explained his findings in a book called Liber Abaci, published in 1202, which had a section devoted to the intriguing sequence which would be named after him hundreds of years later.
Indian poets and musicians had already been aware of the Fibonacci sequence for centuries though, having spotted its implications for rhythm and different combinations of long and short beats.
Mozart made use of the Golden Ratio when writing a number of his piano sonatas. A sonata can be divided into two separate sections, known as the exposition (where the theme is introduced) and the development and recapitulation (where the theme is developed and repeated).
In Mozart’s sonatas, the number of bars of music in the latter section divided by the former is approximately 1.618, the Golden Ratio.
There’s even a style of poetry inspired by the Fibonacci sequence, known as Fib Poetry. Every line of the poem must contain the exact number of syllables that correspond with the Fibonacci sequence. So a six line poem would have syllable line counts of 1, 1, 2, 3, 5 and 8.
Ways to connect
Telegram: @JoelWalbert
Email: thetruthaddict@tutanota.com
The Truth Addict Telegram channel
Hard Truth Soldier chat on Telegram
Mastodon: @thetruthaddict@noagendasocial.com
Session: 05e7fa1d9e7dcae8512eed0702531272de14a7f1e392591432551a336feb48357c
Odysee: TruthAddict
Donations (#Value4Value)
Buy Me a Coffee (One time donations as low as $1)
Bitcoin:
bc1qe8enf89g667dy890j2lnt637xqlt9wvc9f07un (on chain)
bc1qnqjdudgc0qr5yfrp826nxes8kljf9p07mwt3q3yjrd6gqwj0lqtswmy39s (lightning)
nemesis@getalby.com
joelw@fountain.fm
+wildviolet72C (PayNym)
Monero:
43E8i7Pzv1APDJJPEuNnQAV914RqzbNae15UKKurntVhbeTznmXr1P3GYzK9mMDnVR8C1fd8VRbzEf1iYuL3La3q7pcNmeN